Увод
У претходном поглављу је показано да се тачне математичке ситуације за силе које делују флуиди у мировању могу лако добити. То је зато што су у хидростатици укључене само једноставне силе притиска. Када се разматра флуид у покрету, проблем анализе одмах постаје много тежи. Не само да се морају узети у обзир величина и смер брзине честица, већ постоји и сложен утицај вискозности који изазива смицајни или трејни напон између честица флуида у покрету и на границама које их садрже. Релативно кретање које је могуће између различитих елемената флуидног тела узрокује да се притисак и смицајни напон значајно разликују од једне тачке до друге у складу са условима протока. Због сложености повезане са феноменом протока, прецизна математичка анализа је могућа само у неколико, и са инжењерске тачке гледишта, неких непрактичних случајева. Стога је неопходно решавати проблеме протока или експериментисањем или постављањем одређених поједностављујућих претпоставки довољних да се добије теоријско решење. Ова два приступа се међусобно не искључују, јер су основни закони механике увек важећи и омогућавају да се делимично теоријске методе усвоје у неколико важних случајева. Такође је важно експериментално утврдити обим одступања од стварних услова као резултат поједностављене анализе.
Најчешћа поједностављујућа претпоставка је да је флуид идеалан или савршен, чиме се елиминишу компликовани вискозни ефекти. Ово је основа класичне хидродинамике, гране примењене математике која је привукла пажњу еминентних научника као што су Стоукс, Рејли, Ранкин, Келвин и Ламб. Постоје озбиљна инхерентна ограничења у класичној теорији, али пошто вода има релативно низак вискозитет, понаша се као стварни флуид у многим ситуацијама. Из тог разлога, класична хидродинамика се може сматрати највреднијом позадином за проучавање карактеристика кретања флуида. Ово поглавље се бави фундаменталном динамиком кретања флуида и служи као основни увод у наредна поглавља која се баве специфичнијим проблемима који се срећу у грађевинској хидраулици. Изведене су три важне основне једначине кретања флуида, наиме, континуитет, Бернулијева и једначина импулса, и објашњен је њихов значај. Касније се разматрају ограничења класичне теорије и описује се понашање стварног флуида. Претпоставља се нестишљив флуид.
Врсте тока
Различите врсте кретања флуида могу се класификовати на следећи начин:
1. Турбулентно и ламинарно
2. Ротациони и иротациони
3. Стабилно и нестабилно
4. Униформне и неуниформне.
Аксијалне пумпе серије MVS Пумпе са мешовитим протоком серије AVS (вертикалне аксијалне и потопне пумпе за отпадне воде са мешовитим протоком) су модерне производе успешно пројектоване усвајањем стране модерне технологије. Капацитет нових пумпи је 20% већи од старих. Ефикасност је 3~5% већа од старих.

Турбулентно и ламинарно струјање.
Ови термини описују физичку природу тока.
У турбулентном току, кретање честица флуида је неправилно и постоји наизглед хаотична замена положаја. Појединачне честице су изложене флуктуирајућим трансверзалним брзинама тако да је кретање вртложно и синусно, а не праволинијско. Ако се боја убризга у одређеној тачки, она ће се брзо проширити кроз ток. У случају турбулентног тока у цеви, на пример, тренутни снимак брзине на пресеку би открио приближну расподелу као што је приказано на слици 1(а). Стационарна брзина, каква би била забележена нормалним мерним инструментима, је приказана испрекиданим линијама, и очигледно је да турбулентни ток карактерише нестационарна флуктуирајућа брзина суперпонирана на временску стационарну средњу вредност.
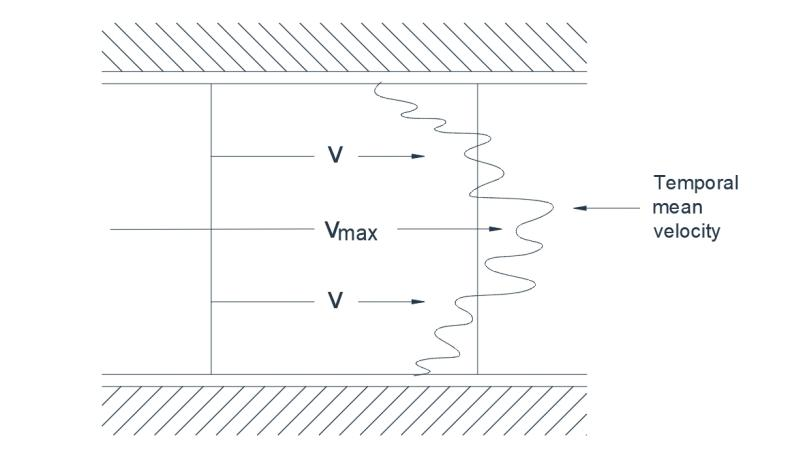
Сл. 1(а) Турбулентни ток
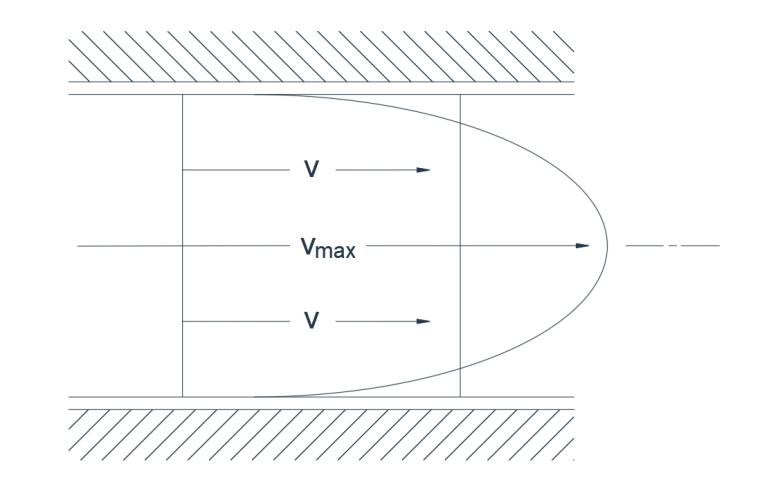
Сл. 1(б) Ламинарни ток
У ламинарном току све честице флуида се крећу паралелним путањама и не постоји попречна компонента брзине. Уређено кретање је такво да свака честица прати тачно путању честице која јој претходи без икаквог одступања. Тако ће танка нит боје остати таква без дифузије. Постоји много већи попречни градијент брзине у ламинарном току (Сл. 1б) него у турбулентном току. На пример, за цев, однос средње брзине V и максималне брзине V max је 0,5 код турбулентног тока и 0,05 код ламинарног тока.
Ламинарни ток је повезан са малим брзинама и вискозним спорим флуидима. У цевоводној и отвореној хидраулици, брзине су скоро увек довољно високе да обезбеде турбулентан ток, иако танак ламинарни слој остаје у близини чврсте границе. Закони ламинарног тока су у потпуности схваћени и за једноставне граничне услове расподела брзине може се математички анализирати. Због своје неправилне пулсирајуће природе, турбулентни ток је пркосио ригорозној математичкој обради, а за решавање практичних проблема неопходно је у великој мери се ослањати на емпиријске или полуемпиријске односе.

Вертикална турбинска ватрогасна пумпа
Број модела: XBC-VTP
Вертикалне пумпе за гашење пожара са дугим вратилом серије XBC-VTP су серија једностепених, вишестепених дифузионих пумпи, произведених у складу са најновијим националним стандардом GB6245-2006. Такође смо побољшали дизајн уз референцу на стандард Америчког удружења за заштиту од пожара. Углавном се користе за снабдевање водом за гашење пожара у петрохемијској, гасној, електранама, памучној текстилној, пристаништима, авијацији, складиштењу, високим зградама и другим индустријама. Такође се могу применити на бродове, морске резервоаре, ватрогасне бродове и друге прилике снабдевања.
Ротациони и иротациони ток.
Проток се назива ротационим ако свака честица флуида има угаону брзину око свог центра масе.
Слика 2а приказује типичну расподелу брзине повезану са турбулентним током поред равне границе. Због неуједначене расподеле брзине, честица чије су две осе првобитно нормалне трпи деформацију са малим степеном ротације. На слици 2а, ток у кружном
путања је приказана, са брзином директно пропорционалном радијусу. Две осе честице се ротирају у истом смеру тако да је ток поново ротациони.
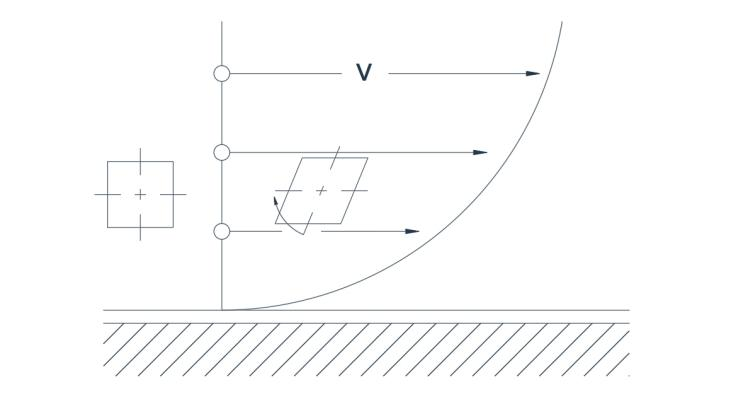
Сл. 2(а) Ротациони ток
Да би ток био иротациони, расподела брзине поред праве границе мора бити равномерна (Сл. 2б). У случају токa у кружној путањи, може се показати да ће иротациони ток постојати само под условом да је брзина обрнуто пропорционална радијусу. На први поглед на Слику 3, ово делује погрешно, али детаљнијим испитивањем се открива да се две осе ротирају у супротним смеровима, тако да постоји компензациони ефекат који производи просечну оријентацију оса која је непромењена у односу на почетно стање.
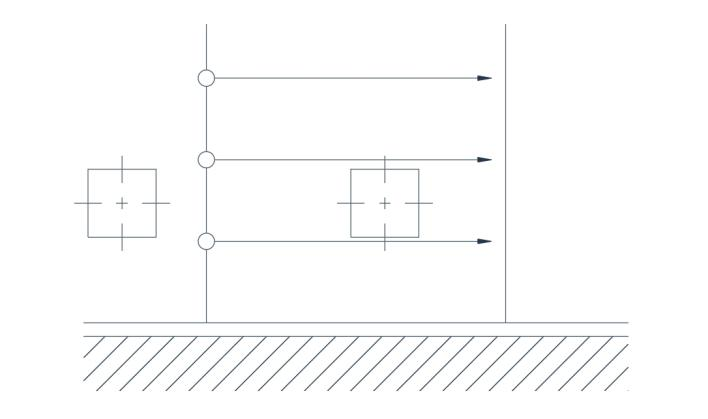
Сл. 2(б) Иротациони ток
Пошто сви флуиди поседују вискозност, стање стварног флуида никада није заиста иротационо, а ламинарни ток је наравно веома ротациони. Стога је иротациони ток хипотетичко стање које би било од академског интереса само да није чињенице да су у многим случајевима турбулентног тока ротационе карактеристике толико безначајне да се могу занемарити. Ово је погодно јер је могуће анализирати иротациони ток помоћу математичких концепата класичне хидродинамике који су раније поменути.
Центрифугална пумпа за морску воду
Број модела: ASN ASNV
Пумпе модела АСН и АСНВ су једностепене центрифугалне пумпе са двоструким усисним системом и сплетним кућиштем и користе се за транспорт течности у водоводним постројењима, циркулацији климатизације, зградама, наводњавању, пумпним станицама за одводњавање, електранама, индустријским системима водоснабдевања, противпожарним системима, бродовима, зградама и тако даље.

Сталан и несталан ток.
Проток се назива стационарним када су услови у било којој тачки константни у односу на време. Строго тумачење ове дефиниције довело би до закључка да турбулентни ток никада није био заиста стационаран. Међутим, за садашњу сврху је погодно посматрати опште кретање флуида као критеријум, а неправилне флуктуације повезане са турбуленцијом само као секундарни утицај. Очигледан пример стационарног тока је константно пражњење у цевоводу или отвореном каналу.
Као последица тога, следи да је ток нестационалан када се услови мењају у односу на време. Пример нестационарног тока је променљиво пражњење у цевоводу или отвореном каналу; ово је обично пролазна појава која следи или наставља стационарно пражњење. Други познати
примери периодичније природе су кретање таласа и циклично кретање великих водених површина у плимном току.
Већина практичних проблема у хидротехници тиче се стационарног тока. То је срећна ситуација, јер временска променљива у нестационарном току знатно компликује анализу. Сходно томе, у овом поглављу, разматрање нестационарног тока биће ограничено на неколико релативно једноставних случајева. Међутим, важно је имати на уму да се неколико уобичајених случајева нестационарног тока може свести на стационарно стање на основу принципа релативног кретања.
Дакле, проблем који укључује пловило које се креће кроз мирну воду може се преформулисати тако да је пловило непокретно, а вода у покрету; једини критеријум за сличност понашања флуида је да релативна брзина буде иста. Поново, кретање таласа у дубокој води може се свести на
стационарно стање претпостављајући да се посматрач креће са таласима истом брзином.

Вертикална турбина, вишестепена центрифугална пумпа за одводњавање воде са линијским вратилом, дизел мотор. Ова врста вертикалне дренажне пумпе се углавном користи за пумпање канализационих или отпадних вода без корозије, на температури мањој од 60 °C, са садржајем суспендованих чврстих материја (не укључујући влакна, гриз) мањим од 150 мг/Л. Вертикална дренажна пумпа типа VTP је део вертикалних водених пумпи типа VTP, а на основу повећања и оковратника, подешава се подмазивање цеви уљем водом. Може да дими на температури испод 60 °C, и да садржи одређена чврста зрна (као што су старо гвожђе и фини песак, угаљ итд.) канализационих или отпадних вода.
Равномерни и неравномерни ток.
Проток се назива равномерним када нема варијација у величини и правцу вектора брзине од једне тачке до друге дуж путање тока. Да би се ускладила са овом дефиницијом, и површина тока и брзина морају бити исте на сваком попречном пресеку. Неравномерни ток се јавља када се вектор брзине мења са локацијом, типичан пример је ток између конвергентних или дивергентних граница.
Оба ова алтернативна услова протока су уобичајена у хидраулици отвореног канала, мада, строго говорећи, пошто се равномерном протоку увек приступа асимптотски, то је идеално стање које се само апроксимира и никада се заправо не постиже. Треба напоменути да се услови односе на простор, а не на време, и стога су у случајевима затвореног протока (нпр. цеви под притиском) потпуно независни од стационарне или нестационарне природе протока.
Време објаве: 29. март 2024.
 sales@tkflow.com
sales@tkflow.com 
